Дизъюнктивная нормальная форма
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.
Формулы в ДНФ:
Формулы не в ДНФ:
Алгоритм построения ДНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения ДНФ
Приведем к ДНФ формулу :

Выразим логические операции → и ↓ через :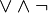
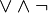
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
Используя закон дистрибутивности, получаем:
Используя идемпотентность конъюкции, получаем ДНФ:
Совершенная дизъюнктивная нормальная форма
Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:
- в ней нет одинаковых элементарных конъюнкций
- в каждой конъюнкции нет одинаковых пропозициональных букв
- каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причём единственная.
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:
 |  |  | 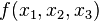 |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
В ячейках результата 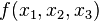 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
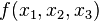 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Первая строка содержит 1 в указанном поле. Отмечаются значения всех трёх переменных, это:
Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: 

Переменные второго члена:
 в этом случае будет представлен без инверсии:
в этом случае будет представлен без инверсии: 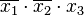
Таким образом анализируются все ячейки 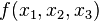 . Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
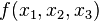 . Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
Совершенная ДНФ этой функции:
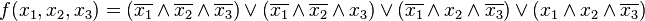
Переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение
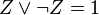 ,
,
после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как  по закону идемпотентности). Например:
по закону идемпотентности). Например:
 по закону идемпотентности). Например:
по закону идемпотентности). Например:
Таким образом, из ДНФ получили СДНФ.

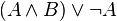



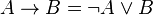
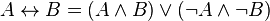
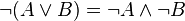

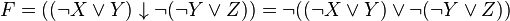

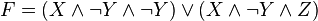
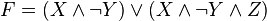
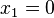


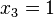
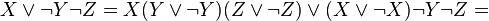


Комментариев нет:
Отправить комментарий